Define Quadratic Function Domain

So the domain of the function is. In algebra quadratic functions are any form of the equation y ax 2 bx c where a is not equal to 0 which can be used to solve complex math equations that attempt to evaluate missing factors in the equation by plotting them on a u shaped figure called a parabola. Therefore the domain of the quadratic function in the form y ax 2 bx c is all real values.

domain list of website domain login or domain location determination url domain level windows server 2019 domain list of stores domain is all x values domain login windows 10 domain local to global

Domain And Range Of A Quadratic Function

How To Find Domain And Range Of Quadratic Functions Youtube

Find Range Of Quadratic Functions

Determining The Domain And Range For Quadratic Functions Texas Gateway

Range Of Quadratic Functions Article Khan Academy

The Vertex Of A Parabola Domain And Range Of A Parabola

Determine the domain and range of the function f of x is equal to 3x squared plus 6x minus 2.

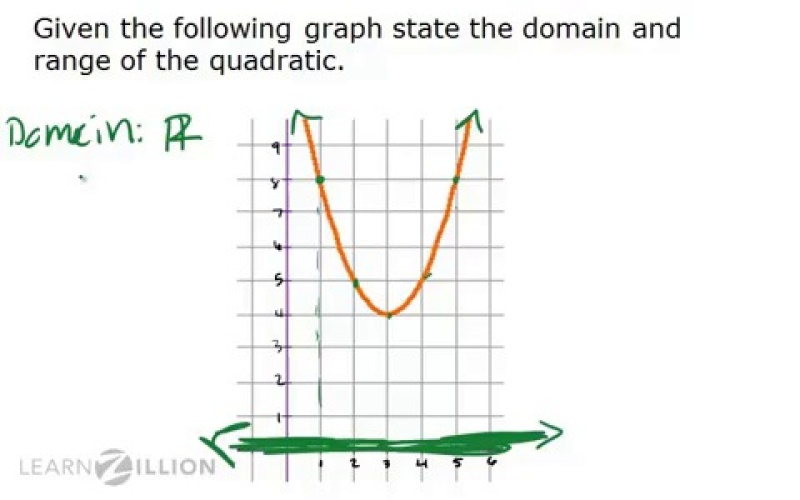
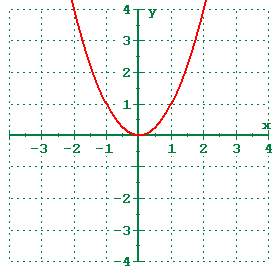
Define quadratic function domain. Finding the domain and range of a quadratic function. Definition of quadratic function. As with any quadratic function the domain is all real numbers. In a quadratic function the greatest power of the variable is 2.

And i can take any real number square it multiply it by 3 then add 6 times that real number and then subtract 2 from it. In the quadratic function y x 2 5x 6 we can plug any real value for x. Because in the above quadratic function y is defined for all real values of x. Y x 2 5x 6.

The domain of a quadratic function in standard form is always all real numbers meaning you can substitute any real number for x. Find the domain and range of f x 5x 2 9x 1. They tend to look like a smile or a frown. Domain of a quadratic function.

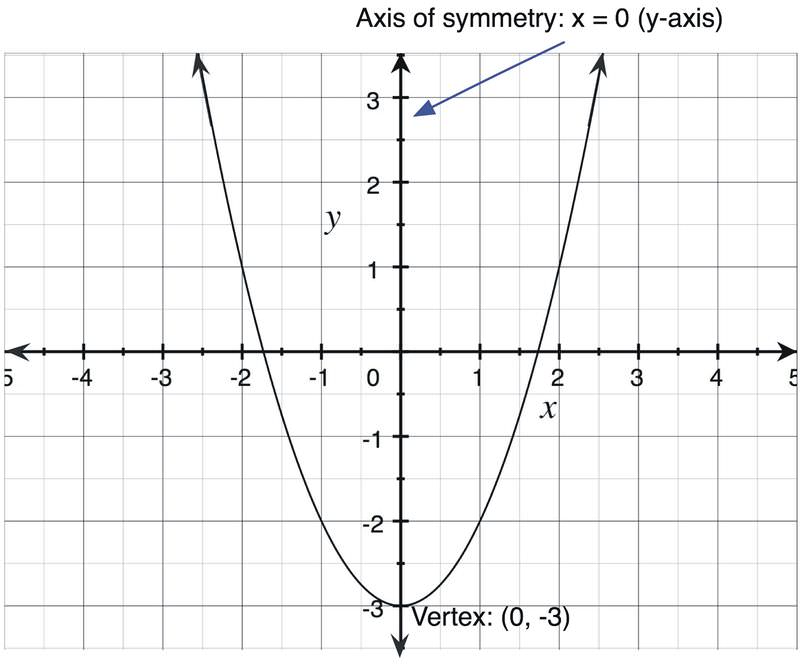
What is a set of all of the valid inputs or all of the valid x values for this function. Quadratic function is a function that can be described by an equation of the form f x ax 2 bx c where a 0. For example a univariate single variable quadratic function has the form in the single variable x the graph of a univariate quadratic function is a parabola whose axis of symmetry is parallel to the y axis as shown at right. We need to determine the maximum value.

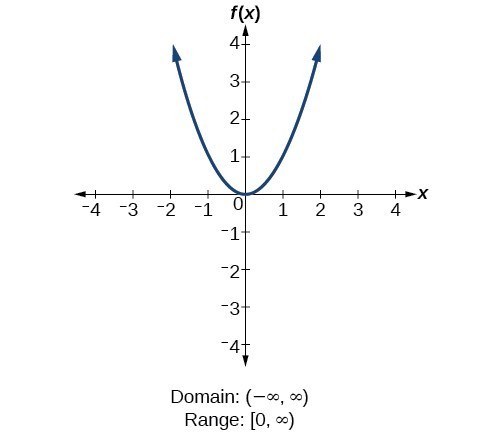
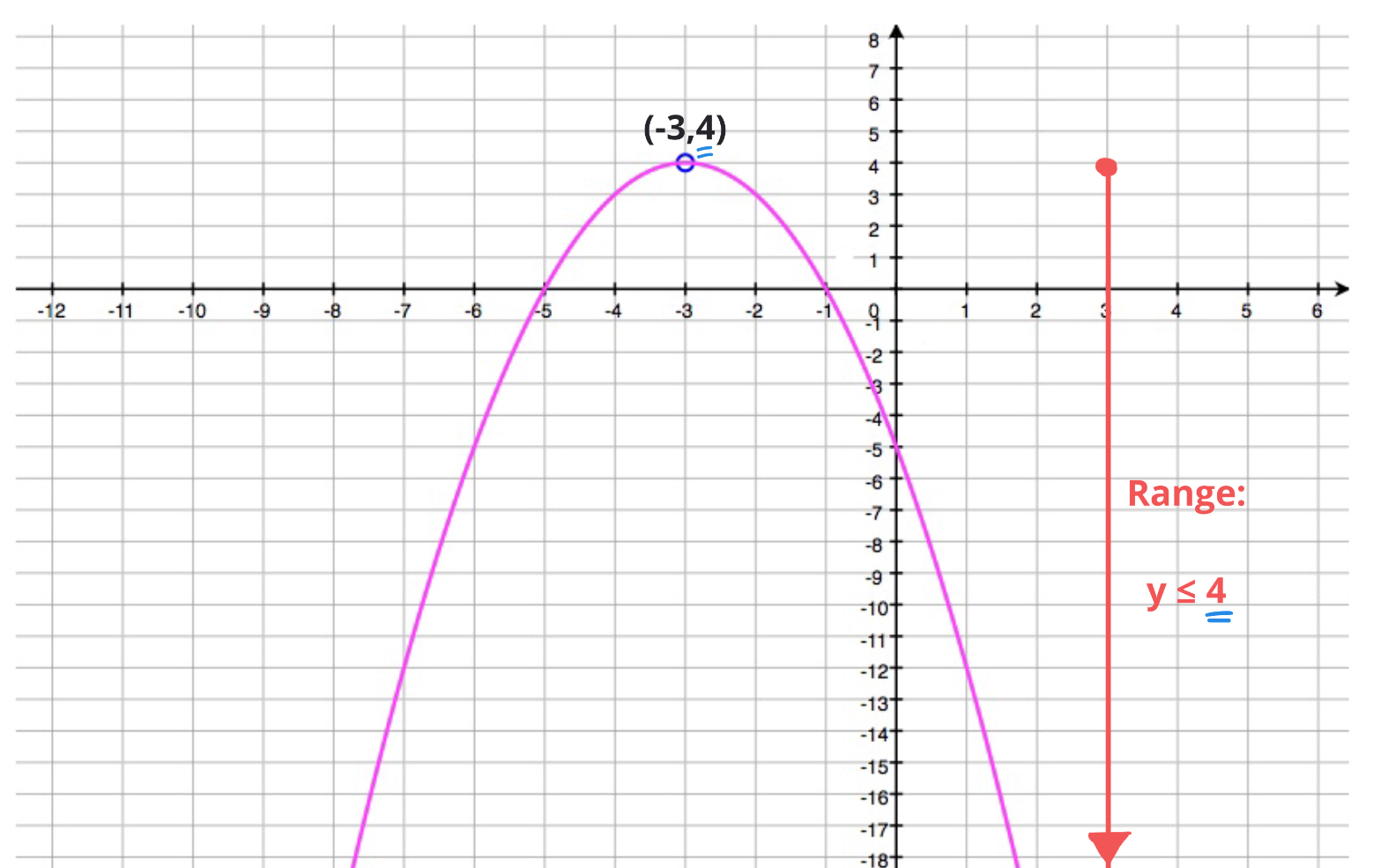
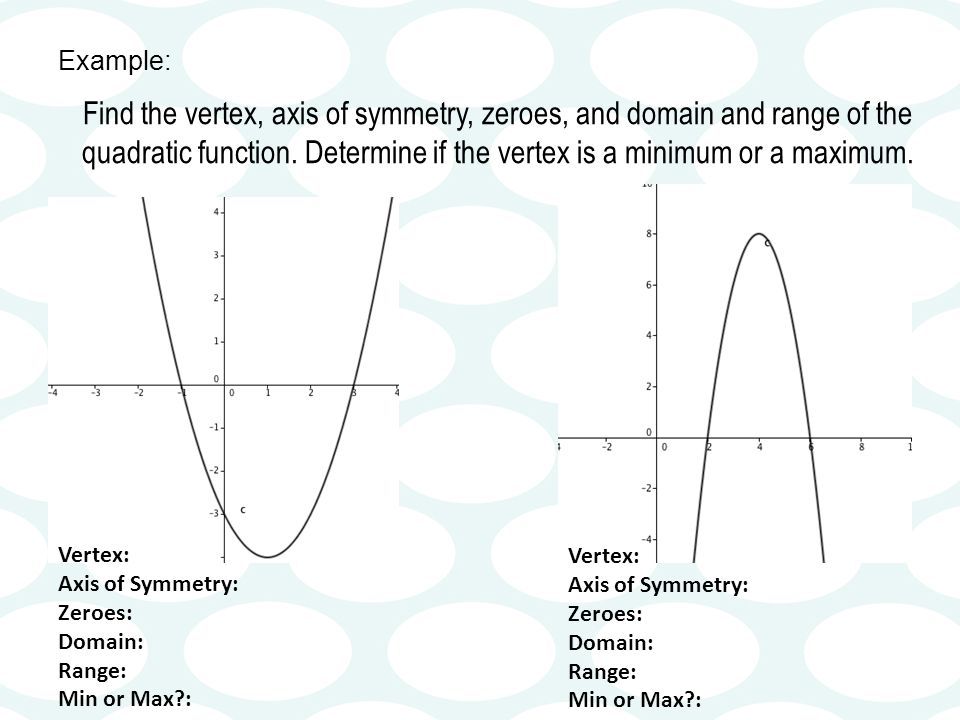
Domain and range of quadratic functions. Given a situation that can be modeled by a quadratic function or the graph of a quadratic function the student will determine the domain and range of the function. Domain and range as with any function the domain of a quadratic function f x is the set of x values for which the function is defined and the range is the set of all the output values values of f. The range of a function is the set of all real values of y that you can get by plugging real numbers into x.

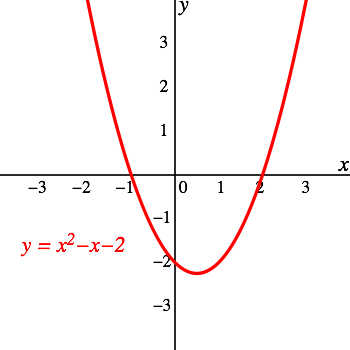
The general form a quadratic function is y ax 2 bx c. Quadratic functions generally have the whole real line as their domain. Find the domain and range of the quadratic function given below. The domain of any quadratic function in the above form is all real values.

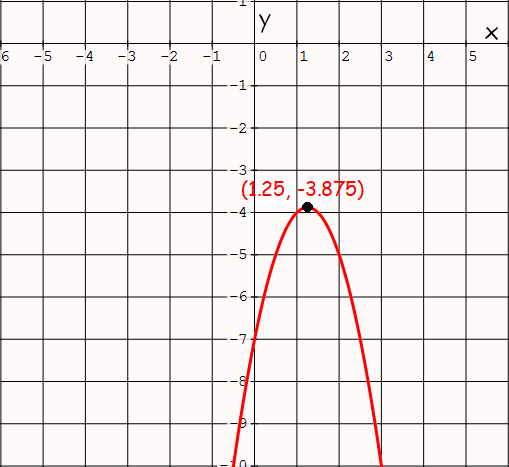
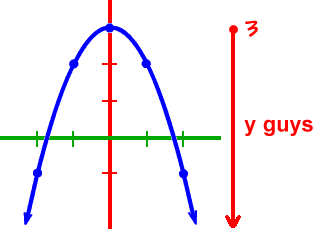
Because a is negative the parabola opens downward and has a maximum value. The graph of a quadratic function is a parabola. Because y is defined for all real values of x. More about quadratic function.

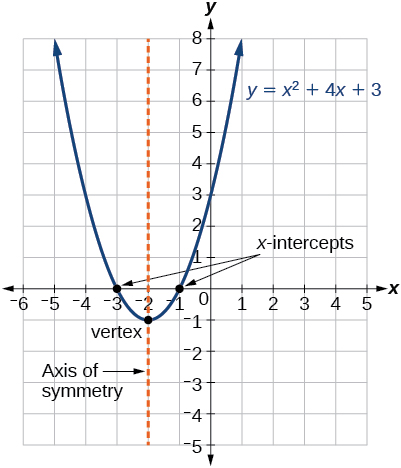
The graphs of quadratic functions are parabolas. If the quadratic function is set equal to zero then the result is a quadratic equation the solutions to the univariate equation are called the roots of the.