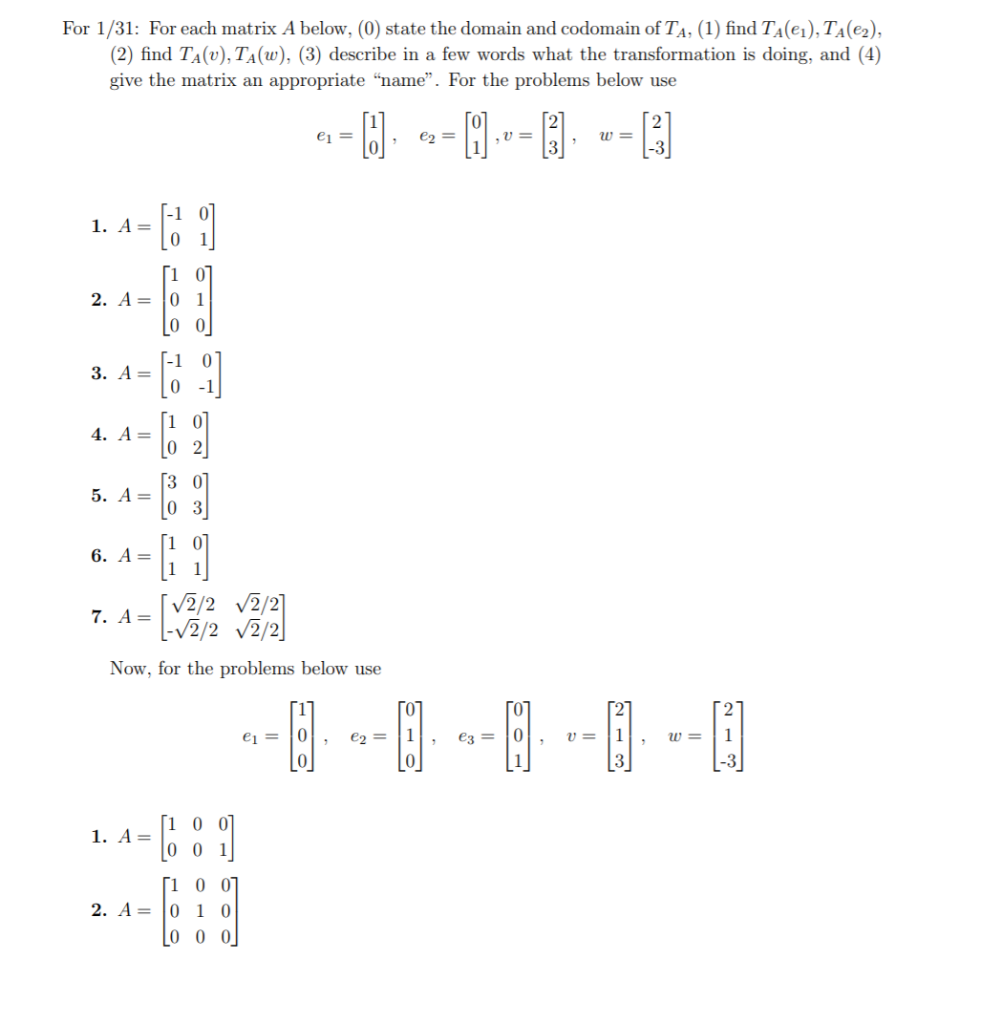Domain And Codomain Matrix

However the image is uncertain. See video guide and some sweet bonus info below. Each matrix represents a map with the domain and codomain.

math domain containing protein namecheap domain and hosting math domain error log2 lua domain specific language meaning of psychomotor domain in english list domain admins cmd list domain controllers linux methods of domain name dispute resolution

Matrix Transformations 1 4 Domain Codomain Range Standard Matrix Passing Linear Algebra Youtube

Domain And Codomain Of Funcion Free Math Worksheets

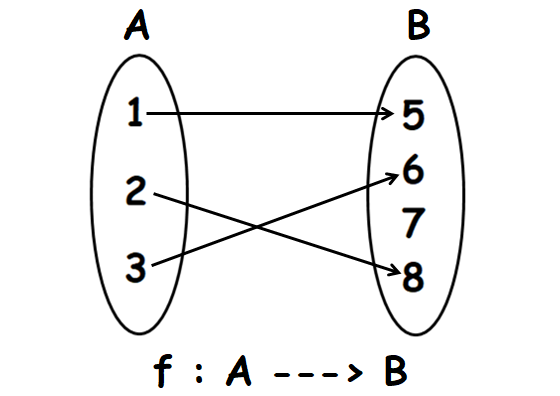
Domain Codomain And Range Of A Function

Linear Algebra Domain And Codomain Of A Matrix Transformation Homeworkhelp

Solved 7 Find The Standard Matrix Domain And Codomain Chegg Com

Has Echelon Form A What Is The Domain And Codoma Chegg Com

The range is the subset of the codomain.

Domain and codomain matrix. And the range is the set of values that actually do come out. The matrix a is 4x6. Reflection dilation rotation shear projection. A matrix can be thought of as a tool to transform vectors.

Some transformations may have image equal to the whole codomain in this case the matrices with rank 2 but many do not instead mapping into some smaller subspace the matrices with rank 1 or 0. The codomain is actually part of the definition of the function. I am asked to find the domain co domain and to determine whether of not the transformation is linear. F x maps the element 7 of the domain to the element 49 of the range or of the codomain.

The codomain and range are both on the output side but are subtly different. Learn to view a matrix geometrically as a function. I m not sure if i am doing this properly so i figured i would ask as my textbook doesn t have solutions. The codomain can be a larger set than the range and is used when the exact range can be hard to specifiy.

If matrix a has 5 columns and 4 rows then by recalling the rules of matrix multiplication we know that x must have 5 rows and 1 column and that the result of the multiplication must have 4 rows and 1 column. 1 20 4 most common. Codomain set b and. The transformation uses matrix multiplication to turn a vector x with 4 elements into a vector with 6.

If someone could explain how to determine the linearity of the system i would appreciate it right now i am just guessing. Understand the vocabulary surrounding transformations. Range r 1 8 64 125 the range should be cube of set a but cube of 3 that is 27 is not present in the set b so we have 3 in domain but we don t have 27 either in codomain or range. Where a is the transformation matrix x is a vector in the domain and y is the resulting vector in the codomain.

Understand the domain codomain and range of a matrix. The answer depends on what you want the codomain range to be if the codomain is to be integers the domain must be x x n2 2n 7 where n is in n if the codomain is to be the real numbers. However the image is uncertain. Domain set a.

For example the function has a domain that consists of the set of all real numbers and a range of all real numbers greater than or equal to zero. Learn examples of matrix transformations. The domain is r 4 and the codomain r 6. Section 3 1 matrix transformations permalink objectives.

The codomain is the set of values that could possibly come out.