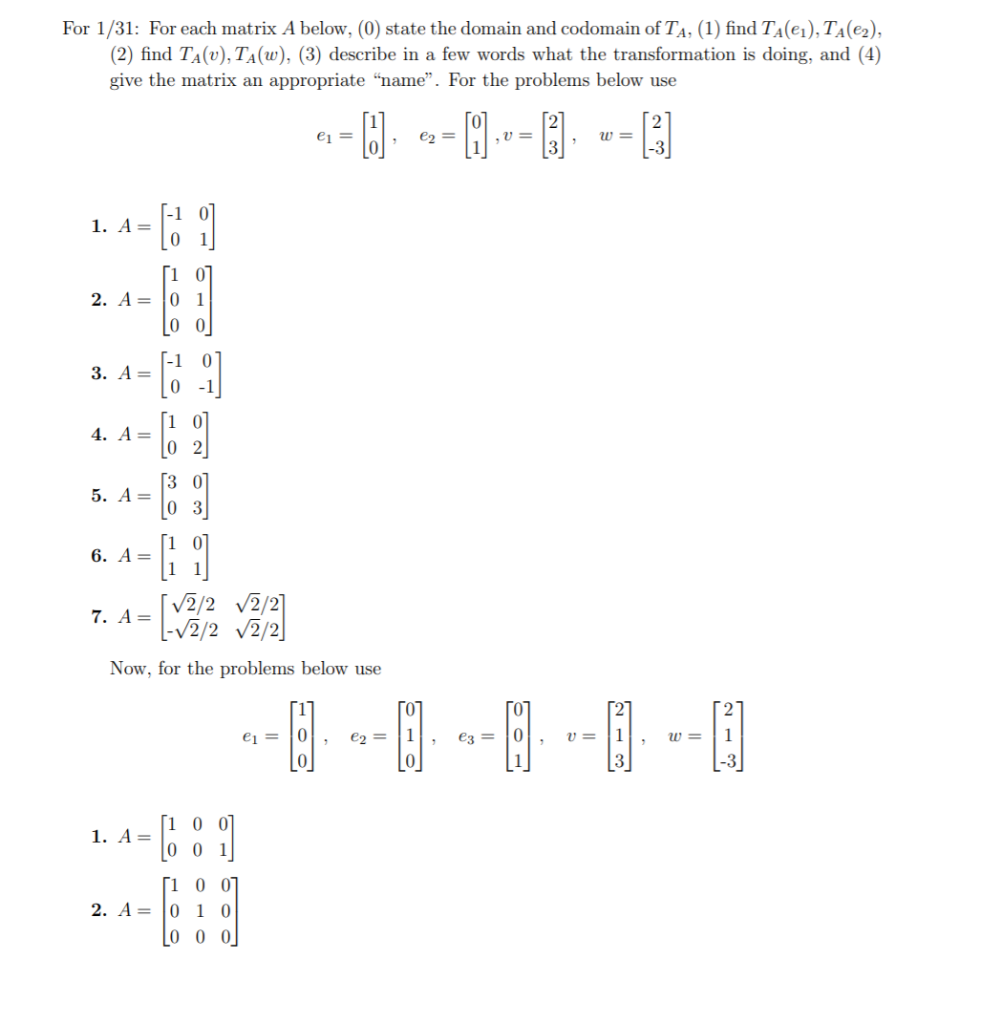Domain And Codomain Of A Matrix

Next we will want to look at two topics in particular.

Domain and codomain of a matrix. Learn examples of matrix transformations. The transformation uses matrix multiplication to turn a vector x with 4 elements into a vector with 6. If matrix a has 5 columns and 4 rows then by recalling the rules of matrix multiplication we know that x must have 5 rows and 1 column and that the result of the multiplication must have 4 rows and 1 column. The matrix a is 4x6.

First if t v to v is a linear operator then it makes sense to consider the matrix m b t m bb t obtained by using the same basis for both domain and codomain. Reflection dilation rotation shear projection. The codomain is actually part of the definition of the function. Where a is the transformation matrix x is a vector in the domain and y is the resulting vector in the codomain.

The answer depends on what you want the codomain range to be if the codomain is to be integers the domain must be x x n2 2n 7 where n is in n if the codomain is to be the real numbers. The codomain can be a larger set than the range and is used when the exact range can be hard to specifiy. The codomain and range are both on the output side but are subtly different. F x maps the element 7 of the domain to the element 49 of the range or of the codomain.

Second we will want to know how this matrix changes if we change the choice of basis. For example the function has a domain that consists of the set of all real numbers and a range of all real numbers greater than or equal to zero. Understand the domain codomain and range of a matrix. Learn to view a matrix geometrically as a function.

And the range is the set of values that actually do come out. The domain is r 4 and the codomain r 6.