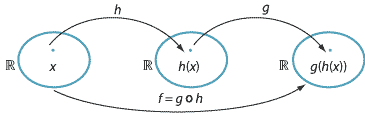
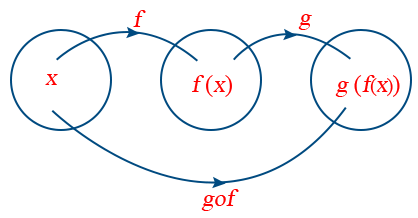
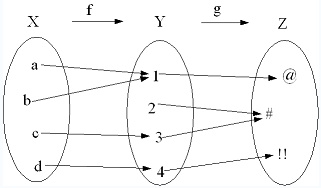
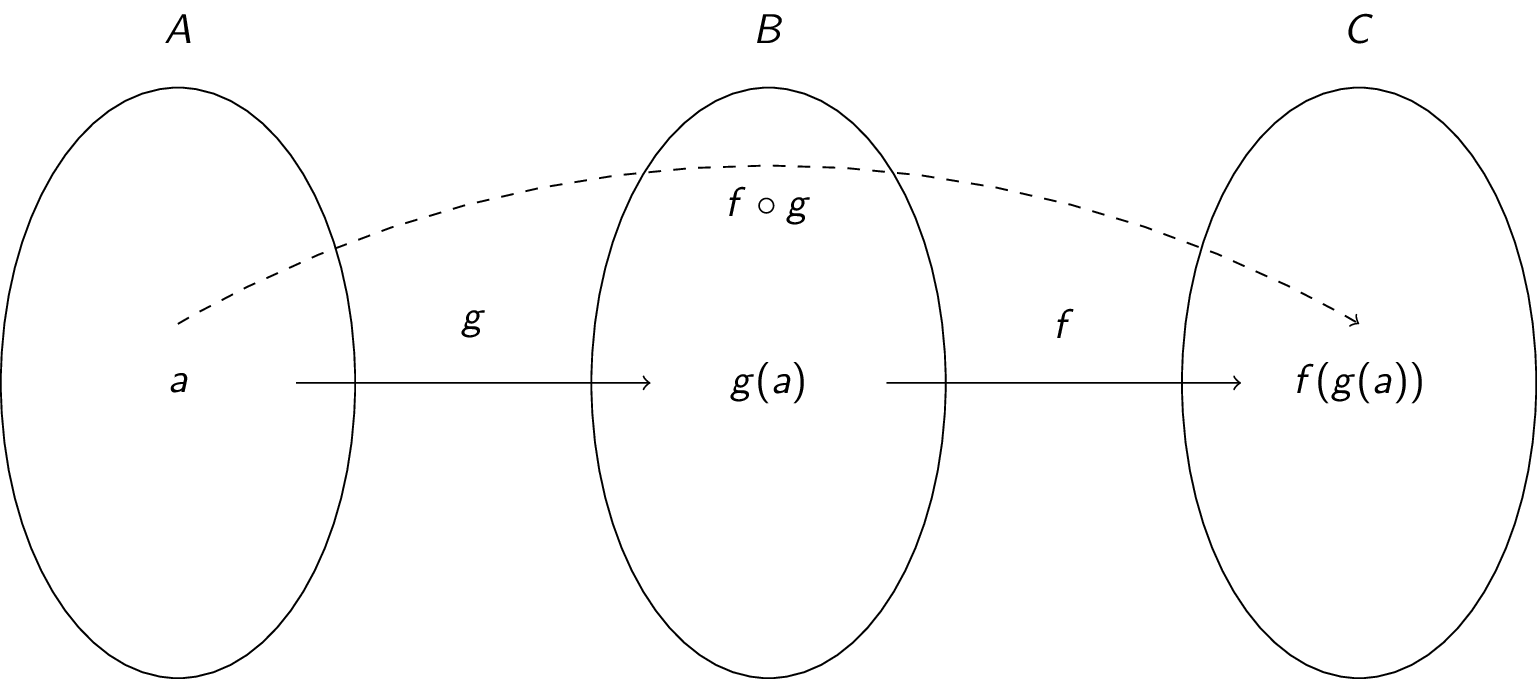
Domain And Codomain Of Composite Function

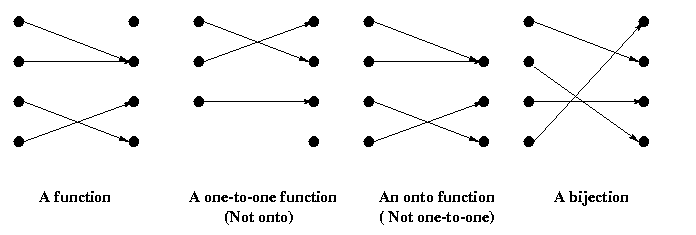
The set of all elements of the form f x where x ranges over the elements of the domain x is called the image of f.

Domain and codomain of composite function. Its range is a sub set of its codomain. All this means is that when we are finding the domain of composite functions we have to first find both the domain of the composite function and the inside function and. Take the function f x x 2 constrained to the reals so f. The yellow oval a subset of this target domain is the range and contains every actual instance of f x.

The image of a function is a subset of its codomain so it might not coincide with it. We can define a function f x 2x with a domain and codomain of integers because we say so. F x maps the element 7 of the domain to the element 49 of the range or of the codomain. We ll be focusing on simple rational functions in this.

For example the codomain of f x must be the set of all positive integers or negative real numbers and so on. The output of a function by redefining the codomain of that function. Every instance of the domain is mapped by the function f into this codomain. The cool thing is that the result is a brand new function with it s own domain and range.

As we discussed previously the domain of a composite function such as latex f circ g latex is dependent on the domain of latex g latex and the domain of latex f latex. But by thinking about it we can see that the range actual output values is just the even integers. An interesting point about the range and codomain is that it is possible to restrict the range i e. It is important to know when we can apply a composite function and when we cannot that is to know the domain of a function such as latex f circ g latex.

The domain of composite functions is the intersection of the domain of the inside function and the new composite function. A codomain is part of a function f if f is defined as a triple x y g where x is called the domain of f y its codomain and g its graph. In this video i will introduce you to finding the domain and range of a composition of two functions. For example the function has a domain that consists of the set of all real numbers and a range of all real numbers greater than or equal to zero.

A function maps elements of its domain to elements of its range.