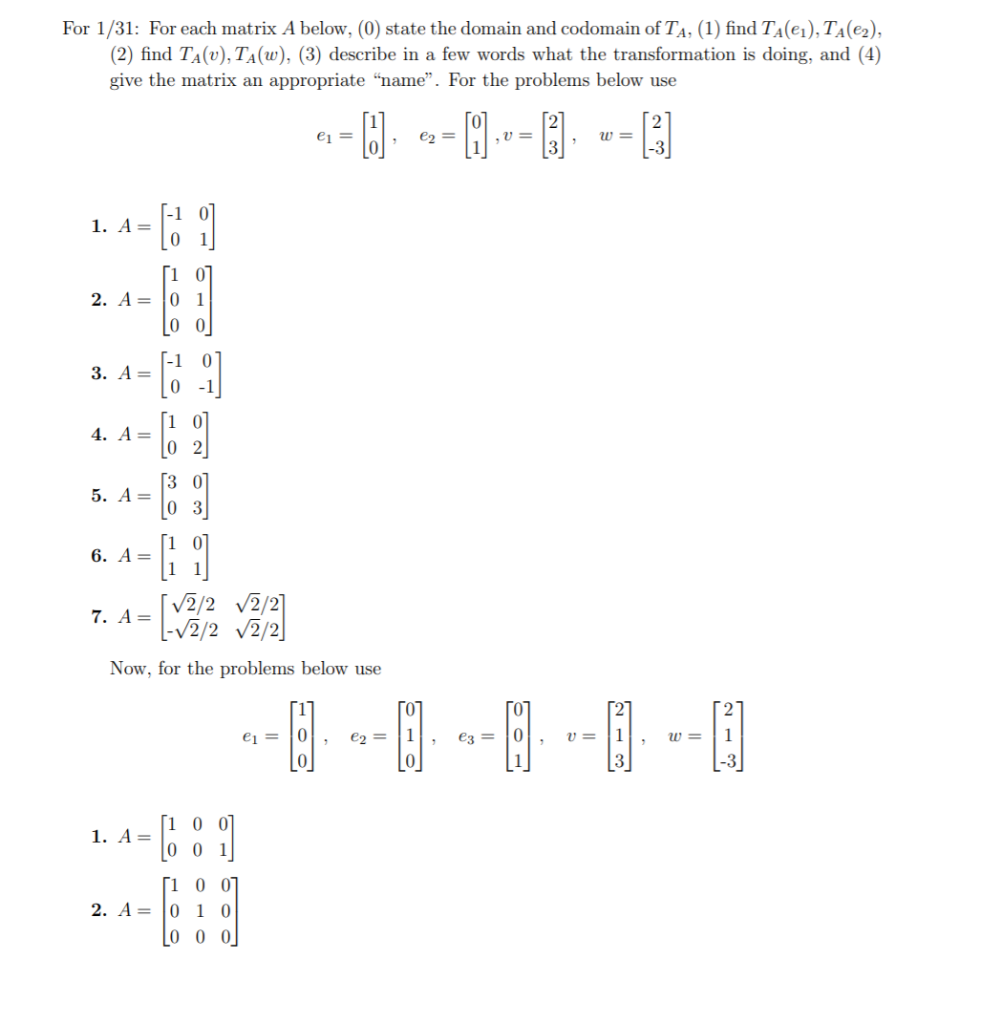Domain Codomain Of The Transformation

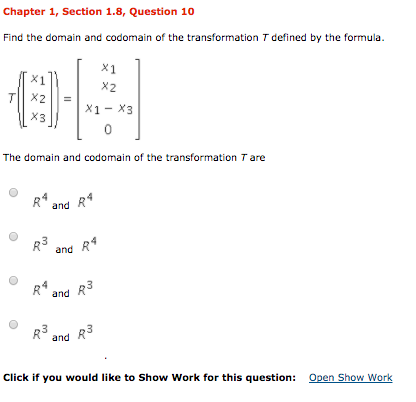
Find the domain and codomain of the transformation t defined by the formula.

Domain codomain of the transformation. A matrix can be thought of as a tool to transform vectors. Domain codomain and range of a function. And the range is the set of values that actually do come out. The codomain and range are both on the output side but are subtly different.

In each part find the domain and codomain of the transformation defined by the equations and determine whether the transformation is linear. A codomain is part of a function f if f is defined as a triple x y g where x is called the domain of f y its codomain and g its graph. R m is called the codomain of t. The codomain can be a larger set than the range and is used when the exact range can be hard to specifiy.

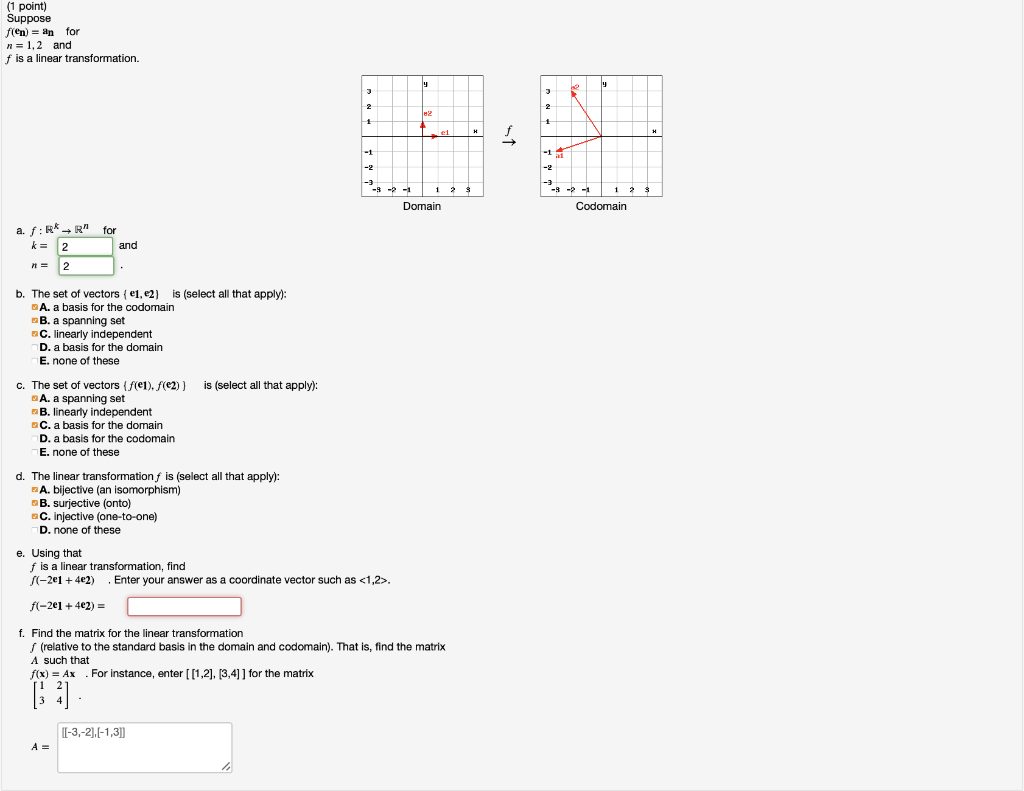
A transformation from r n to r m is a rule t that assigns to each vector x in r n a vector t x in r m. F x maps the element 7 of the domain to the element 49 of the range or of the codomain. The set of all elements of the form f x where x ranges over the elements of the domain x is called the image of f. For x in r n the vector t x in r m is the image of x under t.

R n is called the domain of t. Domain and codomain of the transformation t are. 1 20 4 most common. Converting customary units worksheet.

The image of a function is a subset of its codomain so it might not coincide with it. Instead we simply plug the basis vectors into the transformation and then determine how to write the output in terms of the basis of the codomain. The codomain is the set of values that could possibly come out. R n r m means t is a.

For example the function has a domain that consists of the set of all real numbers and a range of all real numbers greater than or equal to zero. When we compute the matrix of a transformation with respect to a non standard basis we don t have to worry about how to write vectors in the domain in terms of that basis.