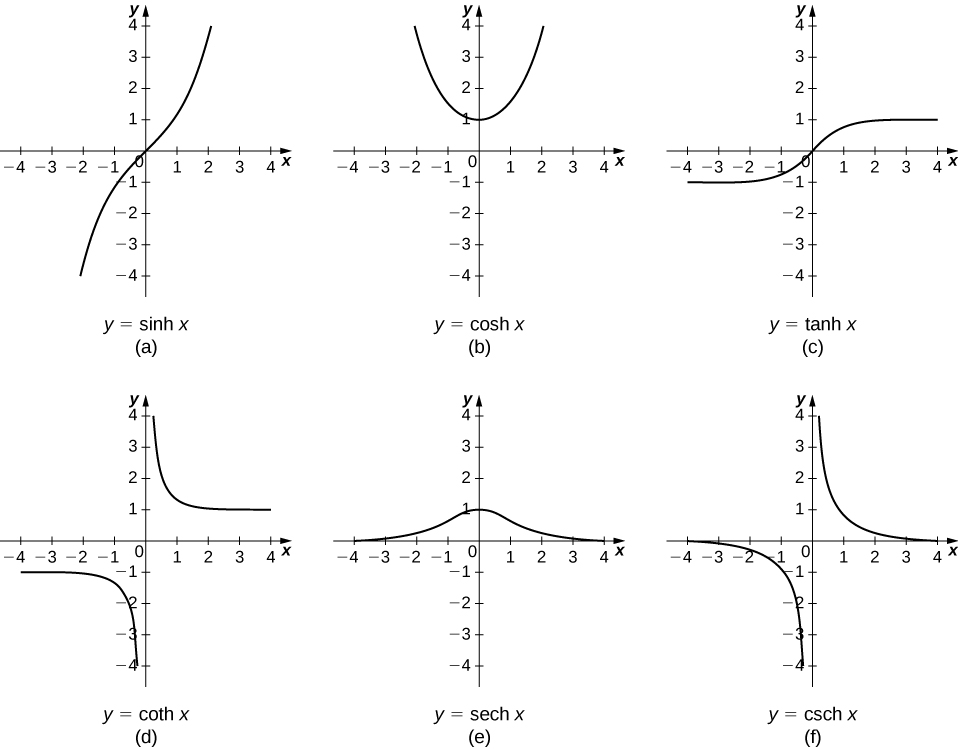
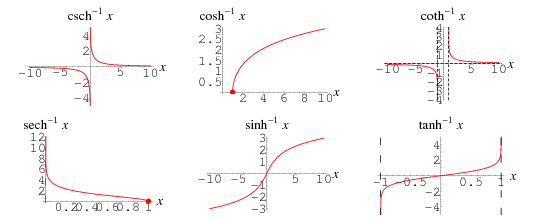
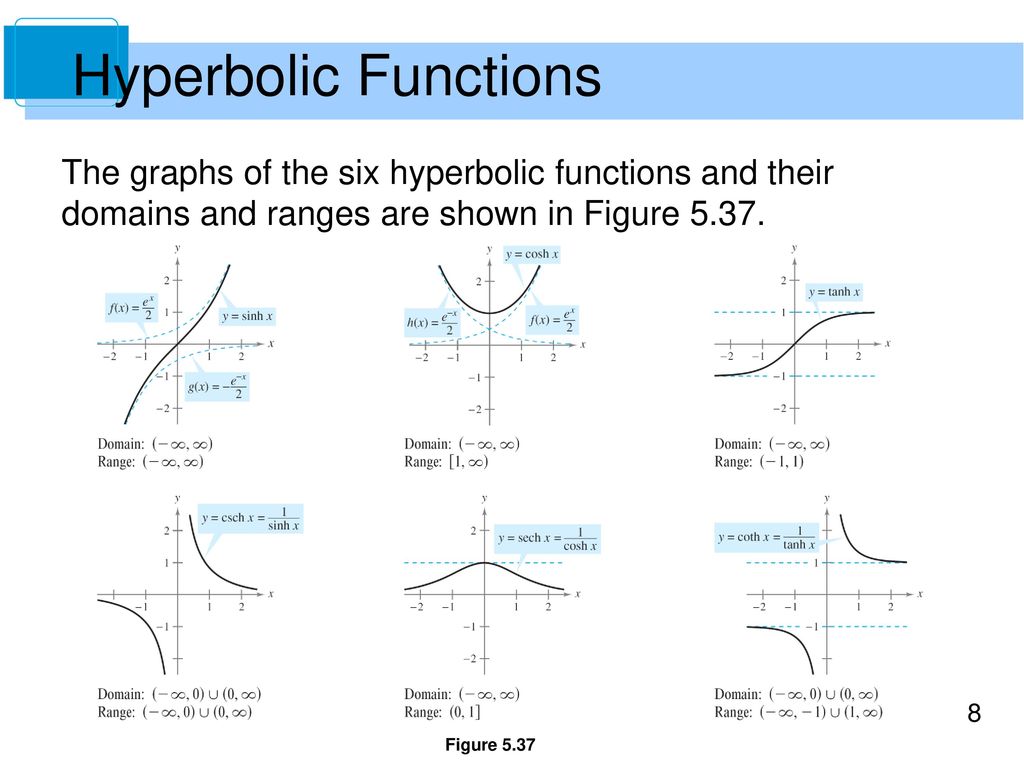
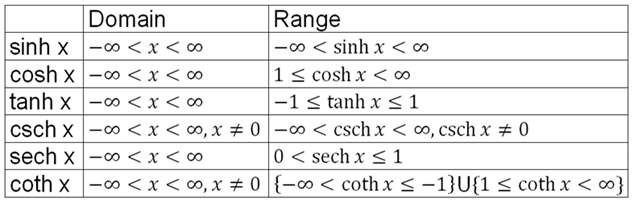
Domain Of A Hyperbolic Function

Out of these the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. The function satisﬁes the conditions sinh0 0 and sinh x sinhx. In complex analysis the hyperbolic functions arise as the imaginary parts of sine and cosine the hyperbolic sine and the hyperbolic cosine are.

domain zone in cpanel domain vs website hosting domain website yang bagus domain with email godaddy domain whois privacy worth it emc data domain default username and password examples of domain specific language domain world set scam

$6 9 Calculus Of The Hyperbolic Functions Mathematics Libretexts$

6 9 Calculus Of The Hyperbolic Functions Mathematics Libretexts

Inverse Hyperbolic Functions From Wolfram Mathworld

Hyperbolic Functions Domain Range Graph And Identities Youtube

5 Logarithmic Exponential And Other Transcendental Functions Ppt Download

Hyperbolic Functions Definitions Identities Derivatives And Inverses Youtube

Answered What Are The Six Basic Hyperbolic Bartleby

$Answered What Are The Six Basic Hyperbolic Bartleby$

The hyperbolic functions take a real argument called a hyperbolic angle the size of a hyperbolic angle is twice the area of its hyperbolic sector the hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector.

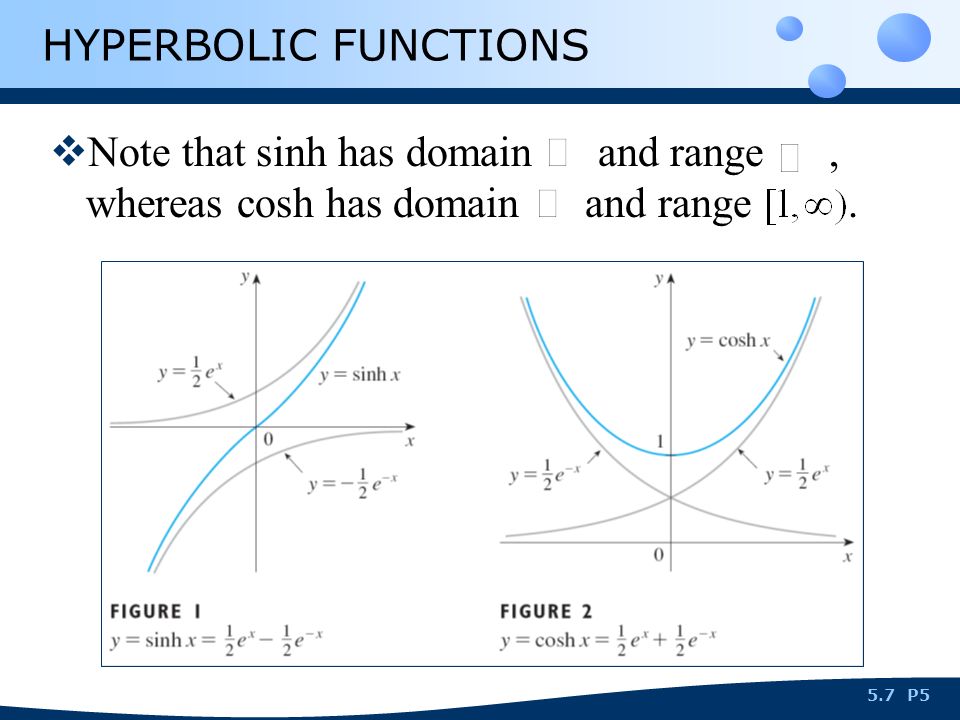
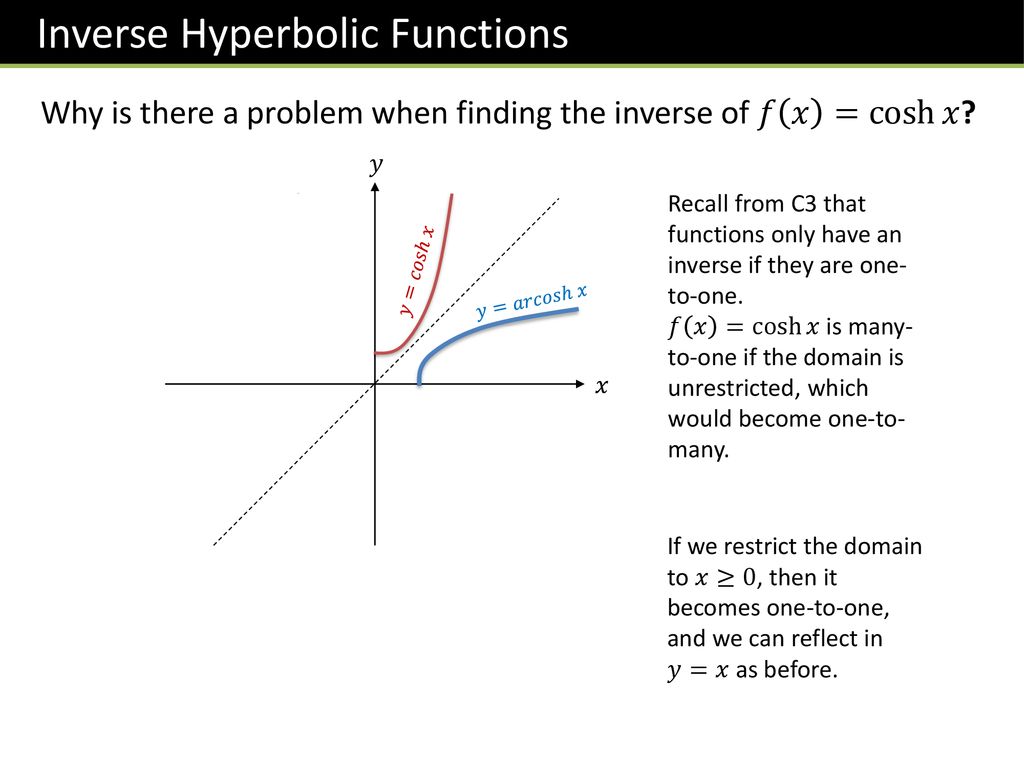
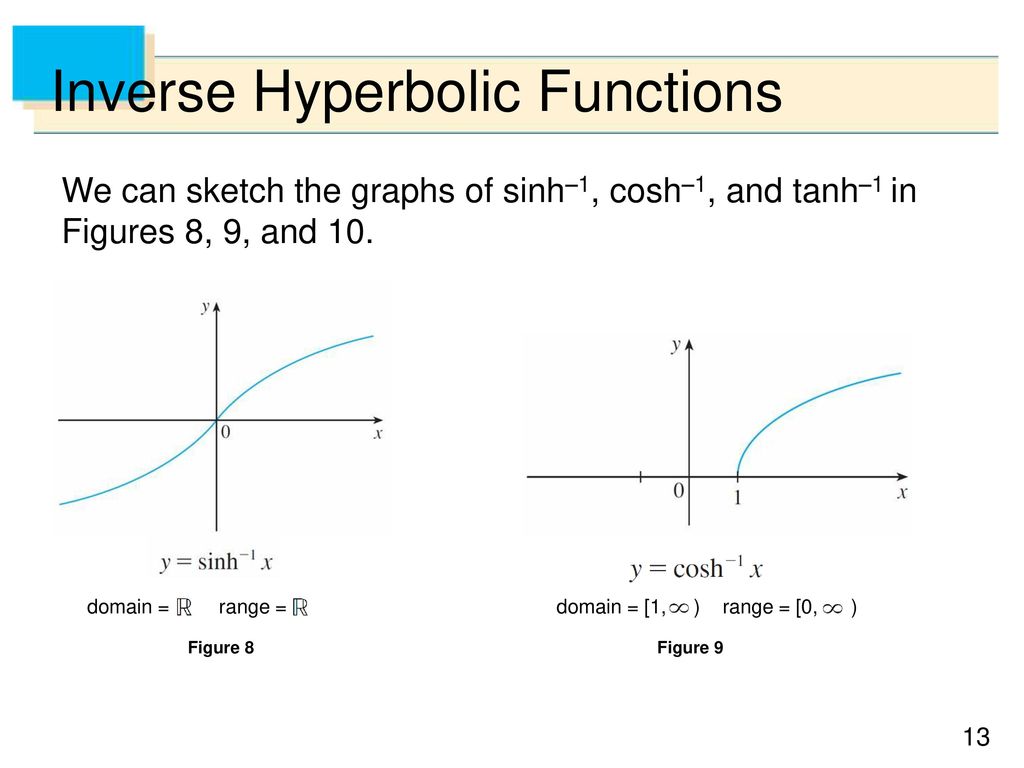
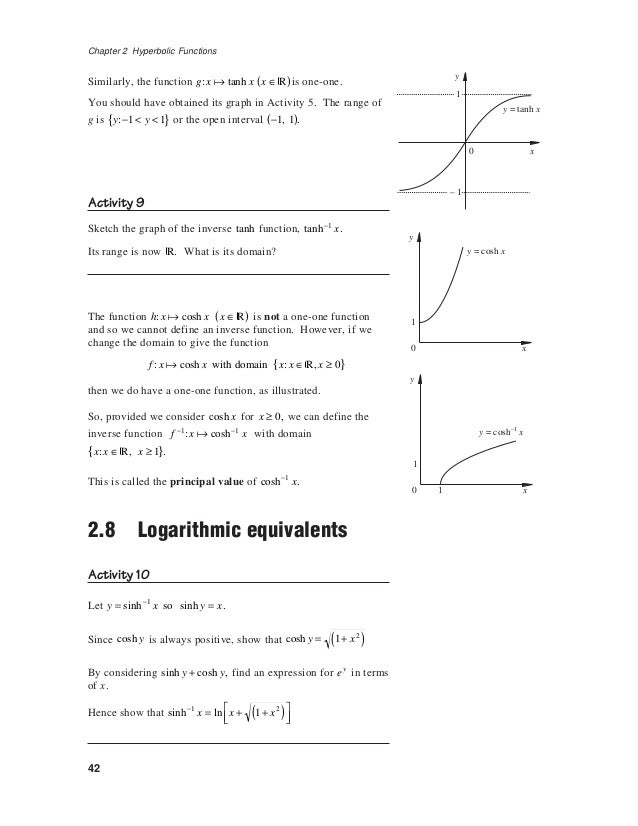
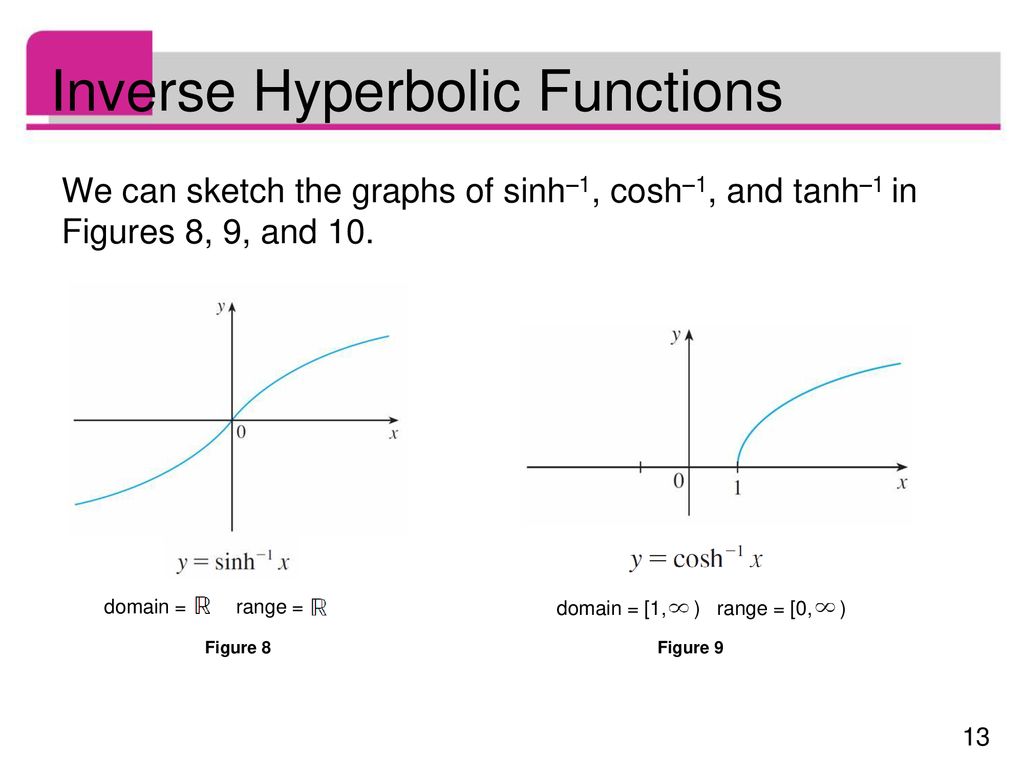
Domain of a hyperbolic function. F x a cosh x a like in this example from the page arc length. One of the interesting uses of hyperbolic functions is the curve made by suspended cables or chains. This website uses cookies to improve your experience while you navigate through the website. The hyperbolic sine function sinh x is one to one and therefore has a well defined inverse sinh 1 x shown in blue in the figure in order to invert the hyperbolic cosine function however we need as with square root to restrict its domain.

This is a bit surprising given our initial definitions. To demonstrate geometric representation of hyperbolic functions we ll draw a hyperbola in cartesian coordinate system. The hyperbolic cosine function written cosh x is defined for all real values of x by the relation cosh x 1 2 ex e x similarly the hyperbolic sine function sinh x is defined by sinh x 1 2 ex e x the names of these two hyperbolic functions suggest that they have similar properties to the trigonometric functions and some of. Hyperbolic function are analogs of trigonometric function and they occur in the solution of many differential or cubic equations.

Definition 4 11 1 the hyperbolic cosine is the function cosh x e x e x over2 and the hyperbolic sine is the function sinh x e x e. 5 c mathcentre january 9 2006. The graph of sinhx is always between the graphs of ex 2 and e x 2. A hanging cable forms a curve called a catenary defined using the cosh function.

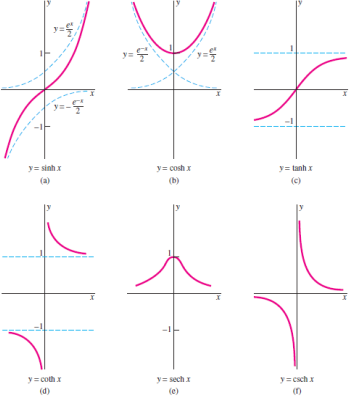
Hyperbolic tangent tanh. From sinh and cosh we can create. The hyperbolic function f x sinhx is deﬁned by the formula sinhx ex e x 2. In contrast to trigonometric functions who form a circle hyperbolic functions relate to a hyperbola.

The hyperbolic functions appear with some frequency in applications and are quite similar in many respects to the trigonometric functions.