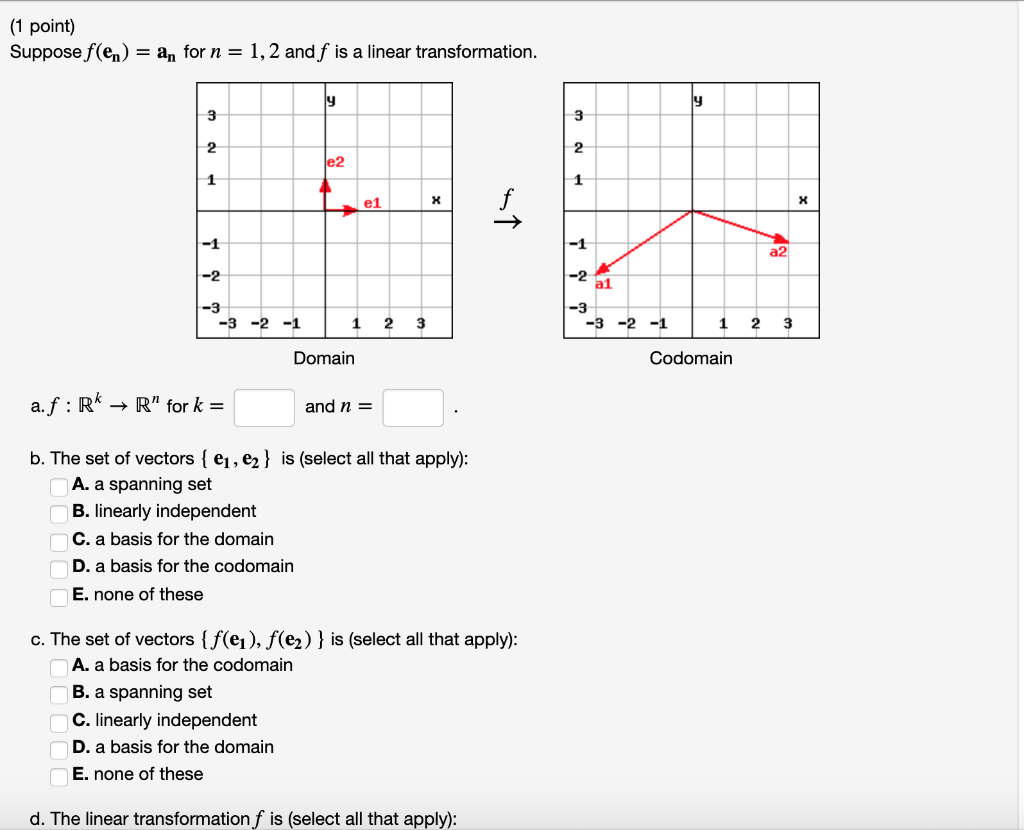
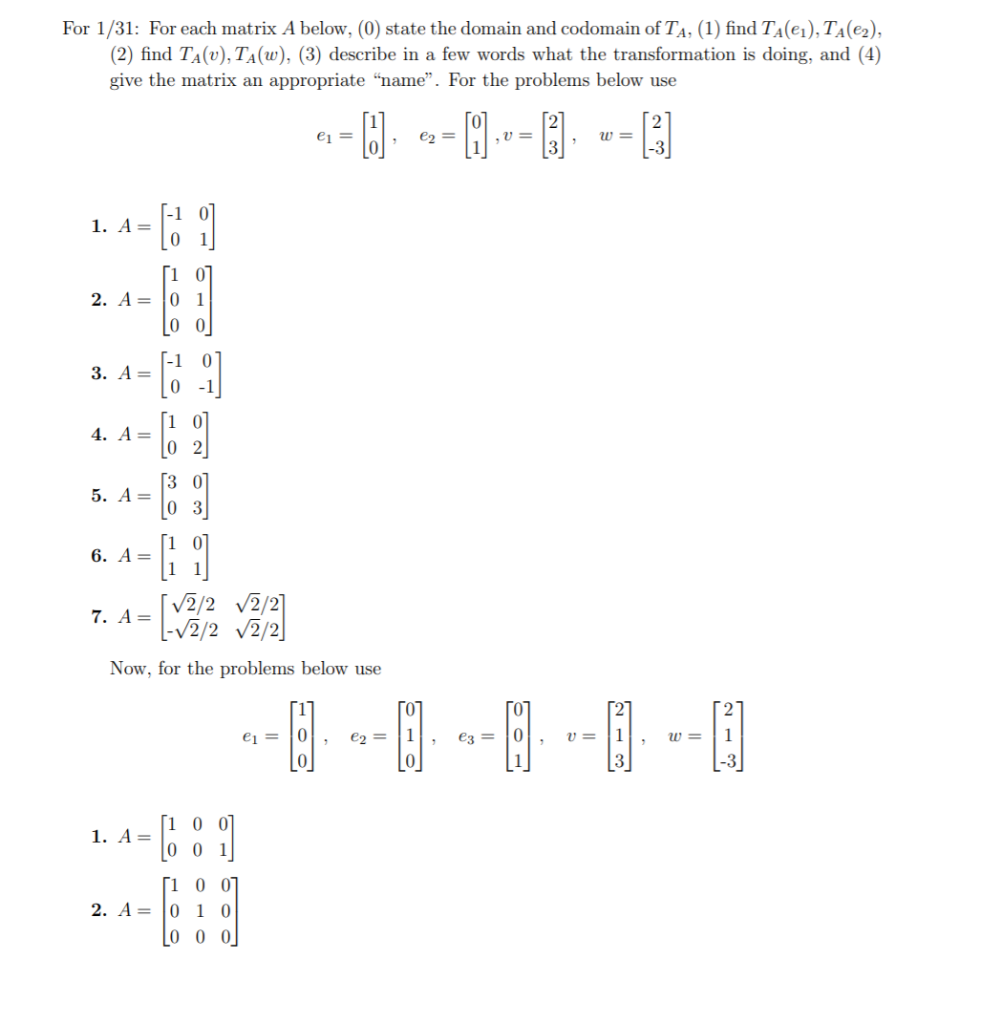Linear Transformation Domain Codomain

The codomain and range are both on the output side but are subtly different. The set of all elements of the form f x where x ranges over the elements of the domain x is called the image of f. Codomain the codomain of a linear transformation is the vector space which contains the vectors resulting from the transformation s action.

domain name meaning and importance domain name of your business domain name means what domain name meaning computer science domain name price au domain name list available domain name lookup cmd domain name ip lookup

Solved For Each Matrix A Define The Linear Transformatio Chegg Com

Solved Consider Linear Transformation I With The Standard Chegg Com

Introductions To Linear Transformations Function T That Maps A Vector Space V Into A Vector Space W V The Domain Of T W The Codomain Of T Chapter Ppt Download

Domain Codomain And Range Of A Function

Solved A 0 0 0 1 View This Matrix As A Linear Transformat Chegg Com

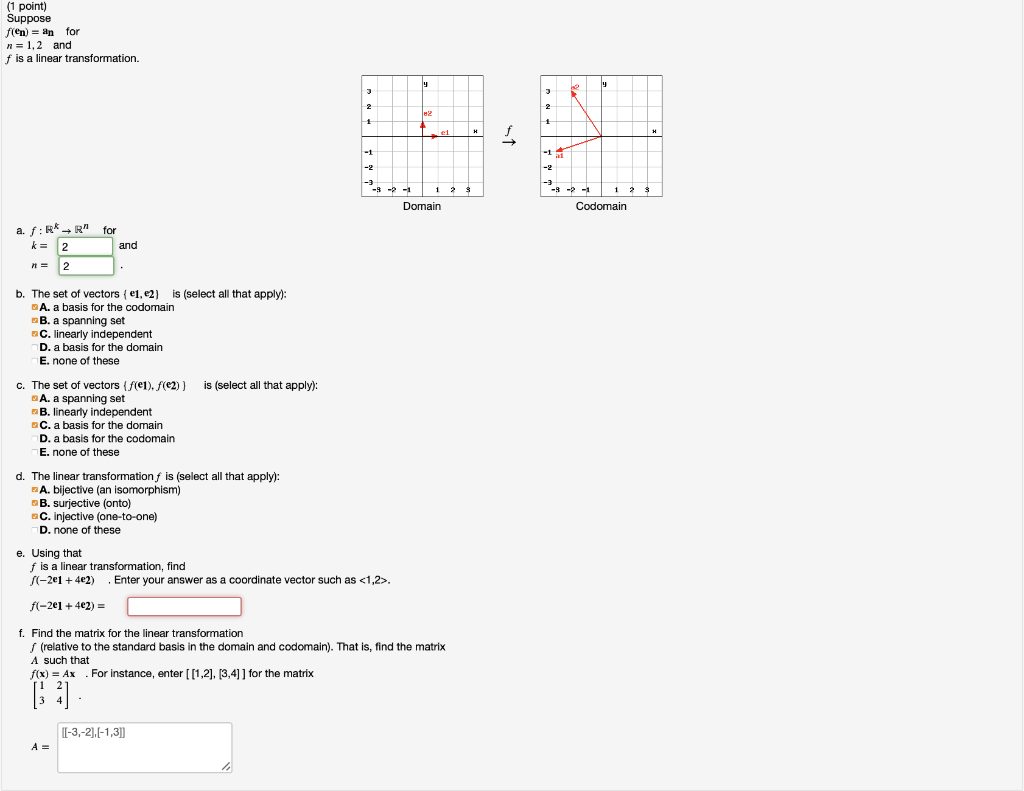
Linear Algebra Domain And Codomain Of A Matrix Transformation Homeworkhelp

1 1 2 1 1 3 t1 3t2 l e2 1 1.

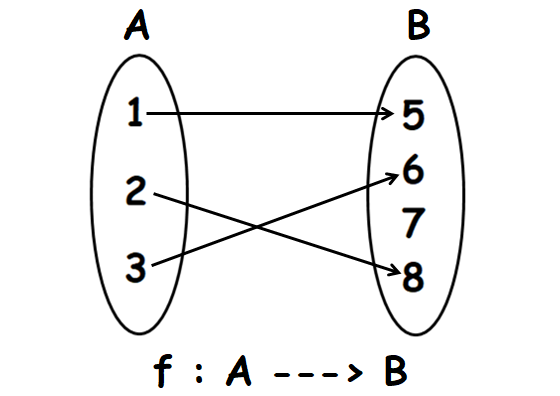
Linear transformation domain codomain. And the range is the set of values that actually do come out. A linear transformation between topological vector spaces for example normed spaces may be continuous. I the range of a linear transformation is a subspace of its codomain. Let v be a vector space.

R2 r2 is a linear transformation l v 1 1. The codomain is actually part of the definition of the function. L e1 1 1. The preimage of y is.

The codomain is the set of values that could possibly come out. Subscribe to this blog. S e1 e2 e 1 0 0 1 t1 t2 is the usual basis just a fancy term for the identity matrix. Follow by email random go.

Rn rm de ned by t x ax where a is an. If f x y then we say y is the image of x. The codomain of the transformation t r 3 r 5 is r 5. A matrix can be thought of as a tool to transform vectors.

1 20 4 most common. V v as t v v for all v v. The image of a function is a subset of its codomain so it might not coincide with it. Thus if t v w then v is a vector in the domain and w is a vector in the range which in turn is contained in the codomain.

Linear trans formations math 240. See video guide and some sweet bonus info below. T 1 is the linear transformation with matrix a 1 relative to c and b. If its domain and codomain are the same it will then be a continuous linear operator.

A linear operator on a normed linear space is continuous if and only if it is bounded for example when the domain is finite dimensional. A codomain is part of a function f if f is defined as a triple x y g where x is called the domain of f y its codomain and g its graph. Y is called the codomain of f. Let e be the usual basis for r2 and let s 2 1 1 1 find the matrix of l relative to the basis s for the domain and e for the codomain of l.

1 1 1 1. I the range of a matrix transformation is the column space of the matrix. X is called the domain of f. Then t is a linear transformation to be called the zero trans formation.

Examples i t. Domain and w the codomain of t.