Domain Of A Quadratic Function Definition

Quadratic functions generally have the whole real line as their domain. Range is all real values of y for the given domain real values values of x. So the domain of the function is.

domain and hosting from google domain and range homework answers domain and range for y x domain and codomain matrix domain and range for y x 2 2 domain and range gcse questions domain and range in a function equation domain and codomain in hindi

Domain And Range Of A Quadratic Function

Quadratic Domain And Range Lessons Tes Teach

How To Find Domain And Range Of Quadratic Functions Youtube

Find Range Of Quadratic Functions

Math 20 1 Chapter 3 Quadratic Functions Ppt Download

The Vertex Of A Parabola Domain And Range Of A Parabola

Domain and range in quadratic functions.

Domain of a quadratic function definition. And i can take any real number square it multiply it by 3 then add 6 times that real number and then subtract 2 from it. The domain of a function is the set of all real values of x that will give real values for y. The range of a function is the set of all real values of y that you can get by plugging real numbers into x. The general form a quadratic function is y ax 2 bx c.

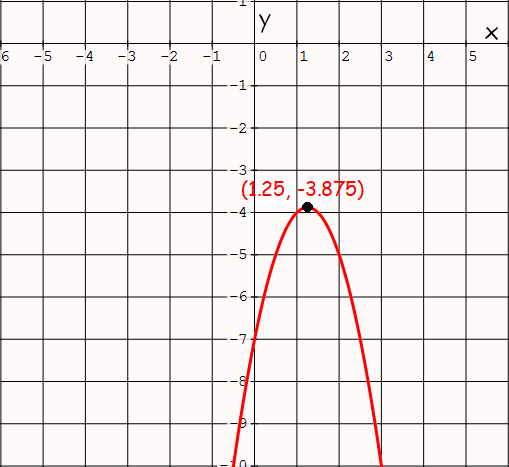
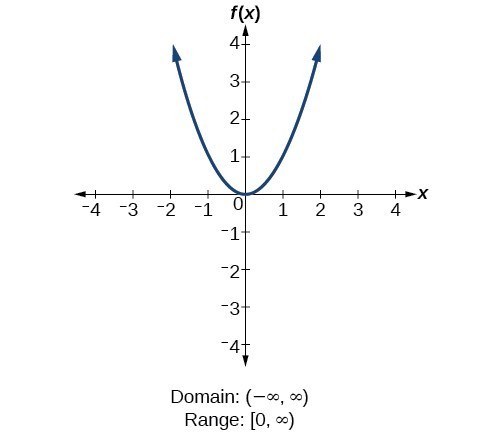
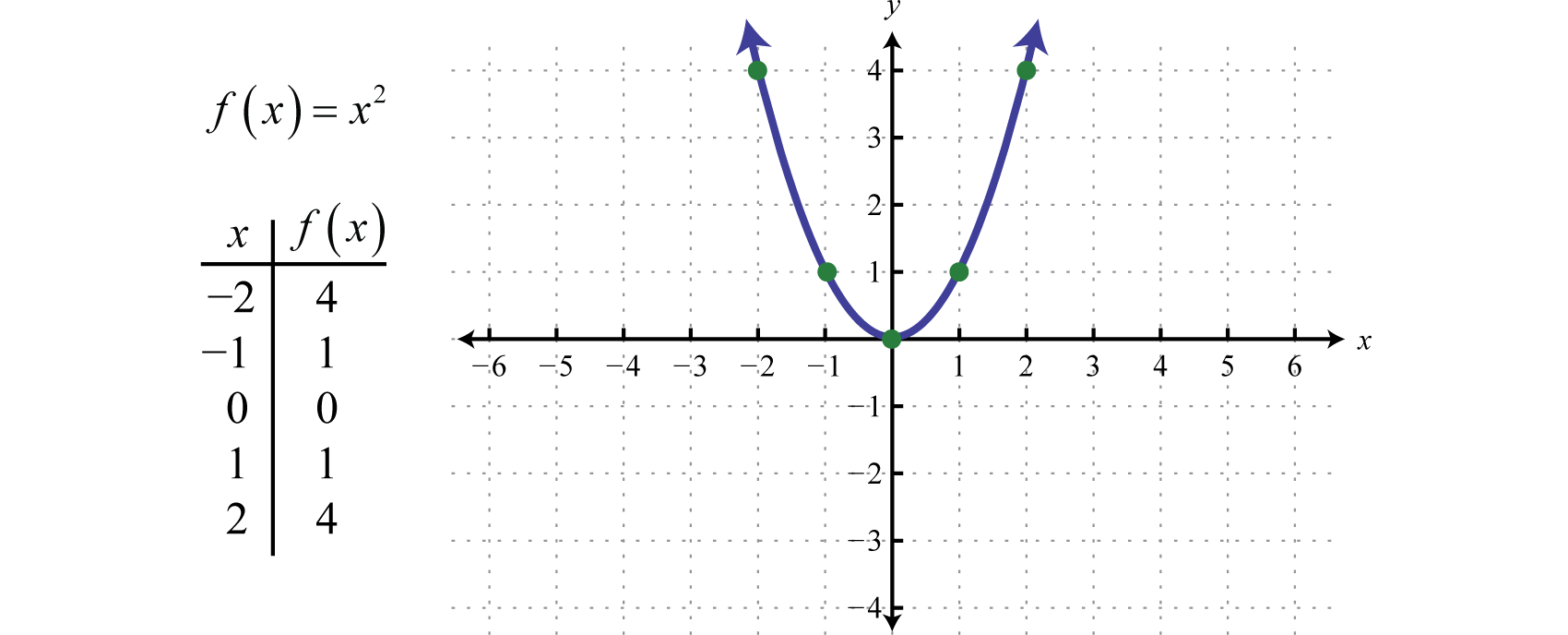
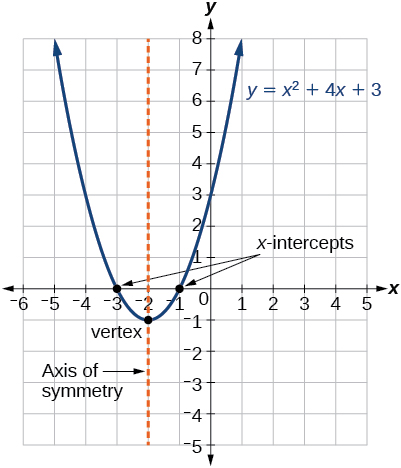
Determine the domain and range of the function f of x is equal to 3x squared plus 6x minus 2. Any x is a legitimate input. The quadratic parent function is y x2. Domain is all real values of x for which the given quadratic function is defined.

What is a set of all of the valid inputs or all of the valid x values for this function. The graph of this function is shown below. The domain of any quadratic function in the above form is all real values. Because y is defined for all real values of x.

For quadratics the domain is all real numbers since there are. Domain is all the x values or independent variable values that give us a real number answer. The domain of a quadratic function in standard form is always all real numbers meaning you can substitute any real number for x. Domain and range of a quadratic functions from mometrix test prep on vimeo.

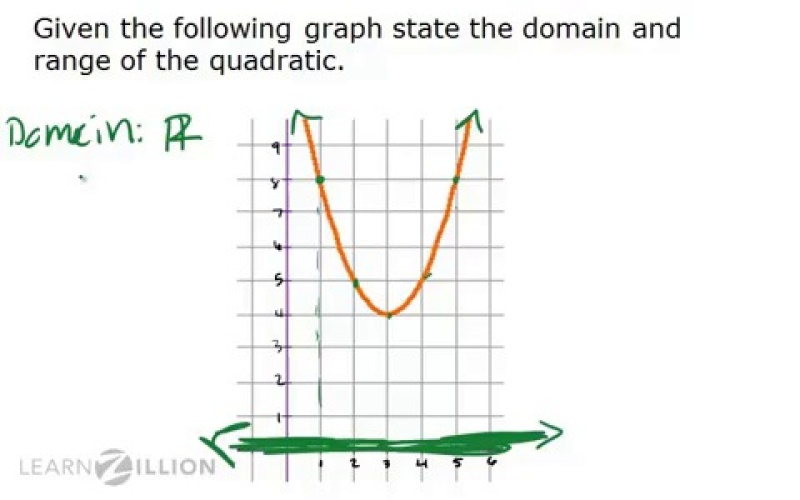
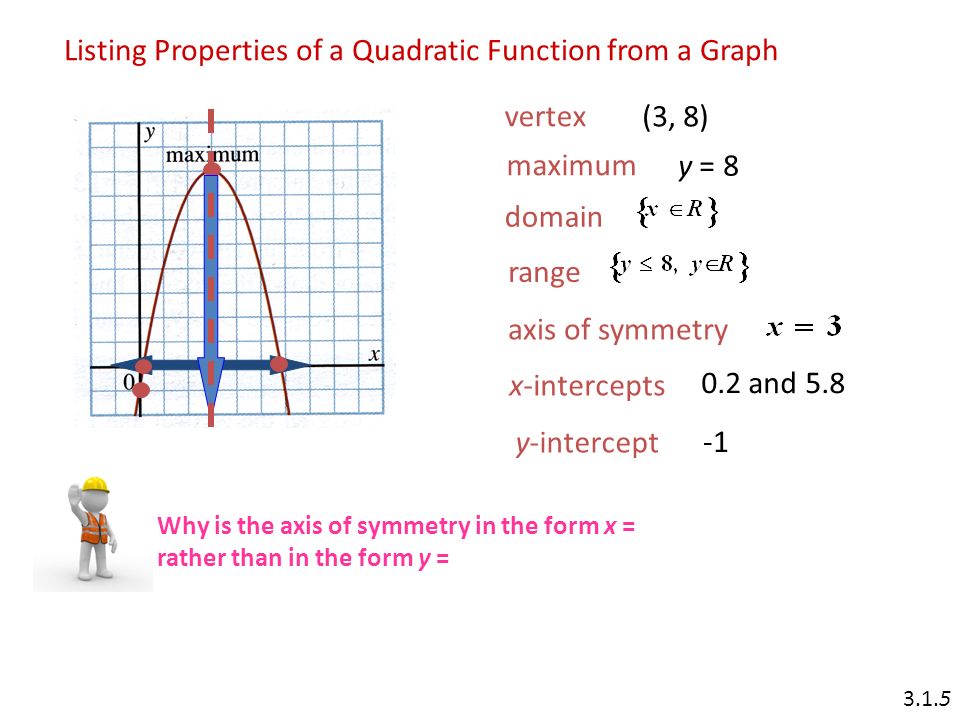
Range with a restricted domain quadratic mooija showed us the rest of problem 8 which is about quadratic functions and therefore takes us back to the original question about range. Therefore the domain of the given quadratic function is all real values. As with any function the domain of a quadratic function f x is the set of x values for which the function is defined and the range is the set of all the output values values of f. There are other parts to number 8.

The range of a function is the set of all real values of y that you can get by plugging real numbers into x. In the quadratic function y x2 5x 6 we can plug any real value for x. Domain of a quadratic function. I have been able to solve them all except for one the last one of number 8.